Sich auf die Arbeiten von Jordan, Noack und Olson stützend, schuf Neville Thiele sein elektromechanisches Ersatzschaltbild des ventilierten Lautsprechers:
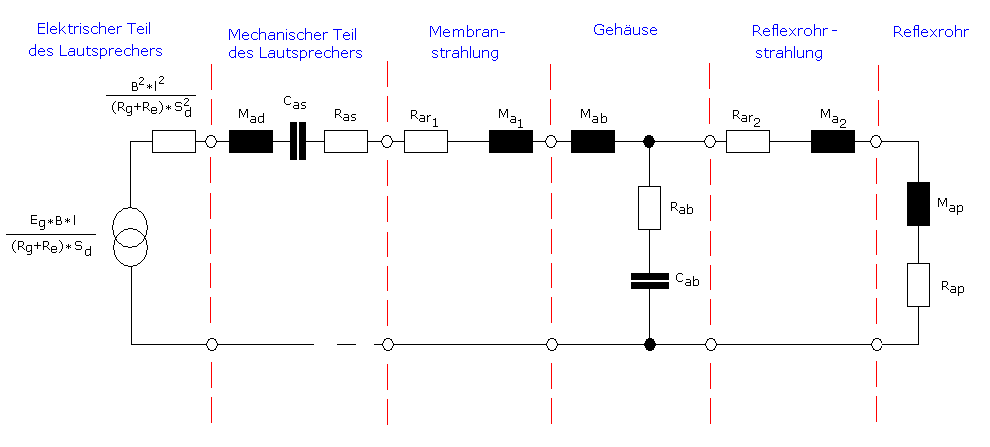
Dieses Modell beinhaltet die elektrische, mechanische und akustische Nachildung des gesamten Lautsprechers. Der Index a (z.B. in 
) bezeichnet das akustische Verhalten des Ersatzschaltbildes. Der Index s (z.B. in 
) steht für speaker, also Lautsprecherchassis. Für box (Gehäuse) wird das b verwendet und p oder v steht für port oder vent, womit das Bassreflexrohr gemeint ist.
Um ein einheitliches Modell zu erhalten werden folgende Transformationsgleichungen benutzt:
Mechanische Impedanz: 
Elektrische Impedanz: 
Akustische Impedanz: 
Dieses Ersatzschaltbild wird nun mit den folgenden Vereinfachungen umgebaut:
und 
können vernachlässigt werden. 
und 
werden aufgrund ihrer, im Vergleich zum Chassis, hohen Güte vernachlässigt.
und 
werden zu: 
Es ergibt sich das vereinfachte akustische Ersatzschaltbild nach Thiele, auf dessen Basis das mathematische Modell begründet ist:
Aufgrund der 4 Reaktanzen im Ersatzschaltbild, handelt es sich um einen Filter 4. Ordnung. Für einen Tiepassfilter lautet die allgemeine Form:
Die Transformation vom Tiefpass− zum Hochpass−Filter erfolgt über: 
Eingesetzt ergibt dies folgende Gleichung: 
Mulitpliziert mit 
ergibt sich: 
(1)
Mit 
, 
und 
ergibt sich der komplexe Frequenzgang:
Aufgeteilt nach Real- und Imginärteil:
Wird der Betrag gebildet ergibt sich dieses Aussehen: 
Das Quadrat des Nenners wird nun aufgelöst: 
Die Klammerausdrücke werden ersetzt durch: 
(1a)
Somit erhält die umgeformte Hochpass−Formel folgendes Aussehen: 
(2)
Die Gleichung (2) wird auf das vereinfachte Ersatzschaltbild von Thiele angewandt. Sie sieht mit den eingesetzten Werten so aus:
(3)
Mit den Umwandlungen: 
sowie 
und 
ergibt sich die vereinfachte Gleichung (4):
(4)
| Durch einen Koeffizientenvergleich mit Gleichung |  |
, lassen sich so die Werte für  und  bis  bestimmen. |
Letztes Update: 12. Mai 2011